意大利著名数学家 Fibonacci 曾提出一个问题:有一对兔子,从出生后第 3 个月起每个月都生一对兔子。小兔子长到第 3 个月后每个月又生一对兔子。按此规律,假设没有兔子死亡,第一个月有一对刚出生的小兔子,问第 n 个月有多少对兔子?
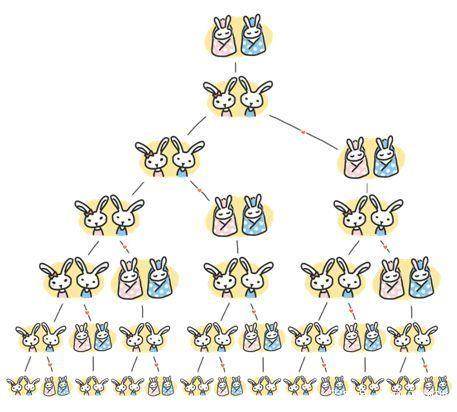
这便是经典的斐波那契数列,因以兔子繁殖为例子而引入,也称为兔子数列,在种子数字 0 和 1 之后,后续的每一个数字都是前面两个数字之和,数列的当前数字与前一个数字的比值无限趋近于黄金分割数 1.61803398875…,故又称为黄金分割数列,0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987。
在数学上,斐波那契数列是以递归的方法定义的:
1
2
3
| F0=0
F1=1
Fn=F(n-1)+F(n-2)(n>=2,n∈N*)
|
初始时刻第 0 个月,没有兔子,即 F(0) = 0 对应没有兔子,第一个月,有一对刚出生的兔子,即 F(1) = 1 对应一对兔子,第二个月,这对兔子还是太小,不会生育,仍然只有一对兔子,从第三个月开始,每个月都会多一对新的兔子,而前两个月的兔子也可以生育,所以兔子的数量就按照斐波那契数列的规律增长,经过 n 个月后,有 F(n) 对兔子
1
2
3
4
5
6
7
8
| function fibonacci(n) {
if(n === 0 || n === 1) {
return n
}
return fibonacci(n - 2) + fibonacci(n - 1)
}
fibonacci(6)
|
1
2
3
4
5
6
7
8
9
10
11
12
| function fibonacci(n) {
if(n === 0 || n === 1) {
return n
}
const fib = [0, 1]
for (let i = 2; i <= n; i++) {
fib[i] = fib[i - 1] + fib[i - 2]
}
return fib[n]
}
fibonacci(6)
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
| function matrixMultiply(a, b) {
const result = []
for (let i = 0; i < a.length; i++) {
result[i] = []
for (let j = 0; j < b[0].length; j++) {
result[i][j] = 0
for (let k = 0; k < a[0].length; k++) {
result[i][j] += a[i][k] * b[k][j]
}
}
}
return result;
}
function matrixPower(matrix, n) {
if (n === 1) {
return matrix
}
if (n % 2 === 0) {
const halfPower = matrixPower(matrix, n / 2)
return matrixMultiply(halfPower, halfPower)
} else {
const halfPower = matrixPower(matrix, (n - 1) / 2)
return matrixMultiply(matrix, matrixMultiply(halfPower, halfPower))
}
}
function fibonacci(n) {
if (n <= 1) {
return n
}
const baseMatrix = [[1, 1], [1, 0]]
const poweredMatrix = matrixPower(baseMatrix, n - 1)
return poweredMatrix[0][0]
}
|
使用斐波那契数列通项公式求解。
1
2
3
4
5
6
| function fibonacci(n) {
const sqrt5 = Math.sqrt(5)
const a = (1 + sqrt5) / 2
const b = (1 - sqrt5) / 2
return Math.round((Math.pow(a, n) - Math.pow(b, n)) / sqrt5)
}
|
注:使用 Canvas 画出斐波那契螺旋线。
